Expected $k$ highest value from $n$ Gaussian draws.
The other day I was writing about chess gender gap, and at some point I had to compute the expected value for $k$-th highest value after drawing $n$ samples from a Gaussian distribution. The paper I was following used an approximation which I felt it was a little bit weird, so I decided to dive a little bit on the topic. Here are some notes about the results.
Bilalic
The methodology followed by Bilalic is based on the idea that the more players in a group, the higher the chance of having a top-performing player. By comparing the expected and actual differences between the top male and female players, the analysis can determine if the gender gap is due to participation imbalance or other factors.
To compute the expected ranking they use the following formula
\[E_{\text{Bilalic}}(k, n) \approx (\mu + c_1 \sigma) + c_2 \sigma \frac{n!}{(n-k)!n^k} (\log n - H(k-1))\]where $c_1 = 1.25$, $c_2 = 0.287$, and $H(k)$ is the $k$-th harmonic number. The formula relies on some assumptions such as normality and big numbers, and its derivation can be found in the original paper.
Blom
At first, I was surprised that the author of the paper had to derive a formula for the $k$ value after $n$ draws from a normal distribution since my intuition told me that this should be a more or less known result. After some googling I discovered this answer, which proposed the formula
\[E_{\text{Blom}}(k, n) \approx \mu + \Phi^{-1} \left( \frac{k - \alpha}{n-2\alpha+1}\right)\sigma\]where $\alpha = 0.375$ and $\Phi^{-1}(x)$ is the inverse cumulative distribution function (also known as the quantile function) of the normal distribution.
Comparison
It’s clear that the two formulas are very different, so the natural question is to wonder if they agree and which one gives better results. To do so I’ve done a simple experiment: given a normal distribution $\mathcal{N}(\mu, \sigma)$ take $n$ draws from $\mathcal{N}$ and compute the average value of the top $k$ rating. Then compute the Blom and the Bilalic values and plot them with the simulated value. I’ve used $n=10000$, $\mu=1800$ and $\sigma=300$ since these are the typical values we are dealing with. The results are in the following plot
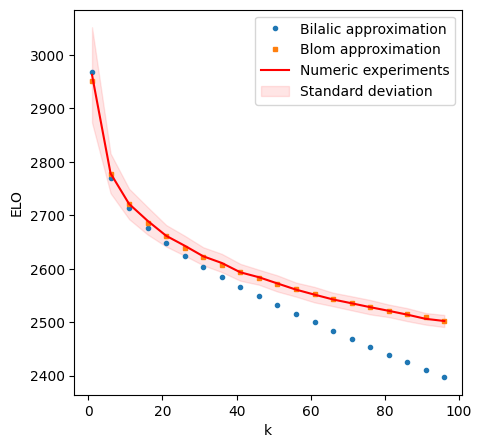
It’s clear that the Blom formula gives better results for large values of $k$.