The least controversial movie

tldr

Escape from Alcatraz is the least controversial movie ever, and The Room is the most controversial.

Background

I tend to discuss a lot with my friends, even more so after a beer or two. I believe our friendship is built upon countless hours discussing almost every topic you can imagine. One of the topics we usually discuss is movies and series. We recommend each other movies or series we enjoyed -or not ¹- and then talk about them. A lot of our discussions end up in an “ask the audience” moment and looking in IMDB at the score of the movie, which usually ends up with one of us saying “Meh, what do people know about good cinema anyway?”. But from time to time a rare event happens and we find a movie we all agree it’s great or it’s bad.

After one of these rare moments, I started wondering about controversial movies and how often people agree on the quality of a cinematographic piece. Imagine you ask people to rate a movie from $0$ to $5$, then a movie with a narrow distribution around its average means that everyone agrees on the quality of the movie, while a movie with a spread rating distribution means that some people love it and some people hate it.

Maths

Mathematically this is: two random variables $A$ and $B$ can have the same mean, ie $\mu_A = \mu_B$ but different variances, ie $\sigma^2_A \neq \sigma^2_B$. It’s clear that the minimum value of $\sigma^2$ is $0$, ie everyone agrees on the quality of the movie, but what about the maximum value? Can we have an upper bound on how much can people disagree on a movie? Formally, this is, given an interval $I = (a, b)$ and a random variable $X$ with support $I$ and average $\mu$, which is the maximum variance $\sigma^2$ that $X$ can have.

To answer this question we first need to understand that $\sigma$ measures how spread are the values of a random variable. Therefore, if we want to maximize the variance of a random variable we need to maximize its spread. In our case the most spread two values can be are $b - a$, ie: one value is $b$ and the other is $a$. So if we want to get the maximum spread we want all our values to be either $a$ or $b$, but with the constraint that the average value should be $\mu$. We can achieve this by assigning a fraction $f$ of votes to $a$ and a fraction $1-f$ to b. Using the average constraint we get

which means $f = \frac{b-\mu}{b-a}$.

The variance is defined as $\sigma^2 = E\left[X^2\right] - E\left[X\right]^2$, where we already know $E[X] = \mu$. Using the value we got for $f$ we can compute the expected value of $X^2$ and get

which means

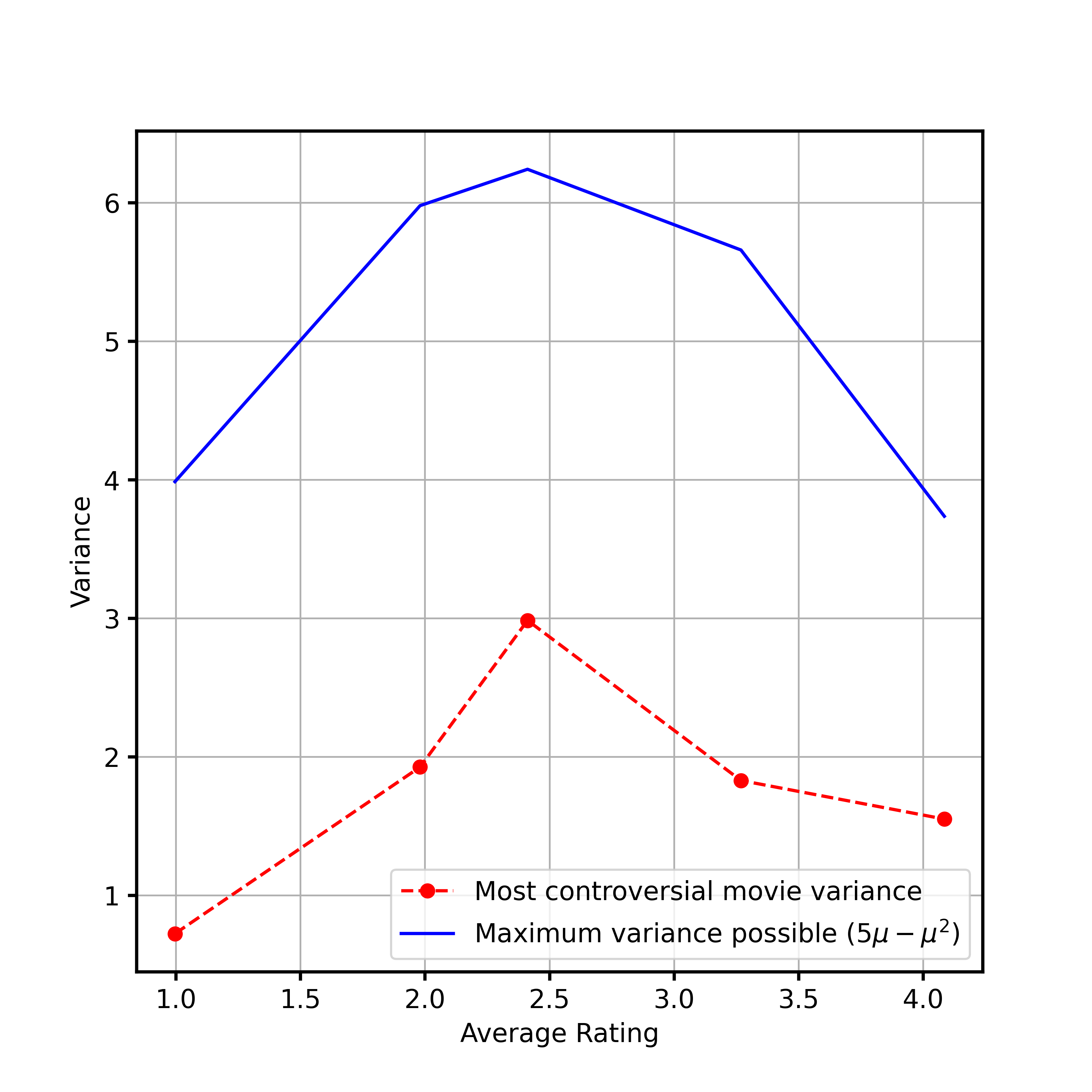
This value is in agreement with Bhatia-Davis inequality , which is a nice check. In our case, we have $a=0$ and $b=5$ so the expression simplifies to $\sigma^2 = 5\mu - \mu^2$. This means that movies with average scores around $0$ or $5$ have a maximum variance smaller than values around the middle, which makes sense intuitively (to get a low/high score you need everyone to agree on your quality). Notice also that the maximum variance you can get is $\sigma^2 = 2.5$.

Data

So far we have done some maths around the concept of being controversial but as someone said “In God we trust, all the others must bring data”, and thanks to God we are in the era of data. A quick search takes us to the Movies Dataset in Kaggle with 26 million ratings from 270,000 users for 45,000 movies, and we’ll use this dataset to ask and answer questions about the least and most controversial movies.

Before starting to answer questions I’ll filter out movies with less than $300$ reviews. If you want to do an EDA of the data feel free to do so, but I won’t do it here ².

Least controversial movies

As we have been saying before we’ll define the “controversiality” of a movie as the variance of the ratings given by users, this is, for two movies with the same average rating we will say the most controversial is the one with the highest rating variance.

Having said so here I present you the least controversial movies in history

Title                | mean | std  
---------------------|------|------
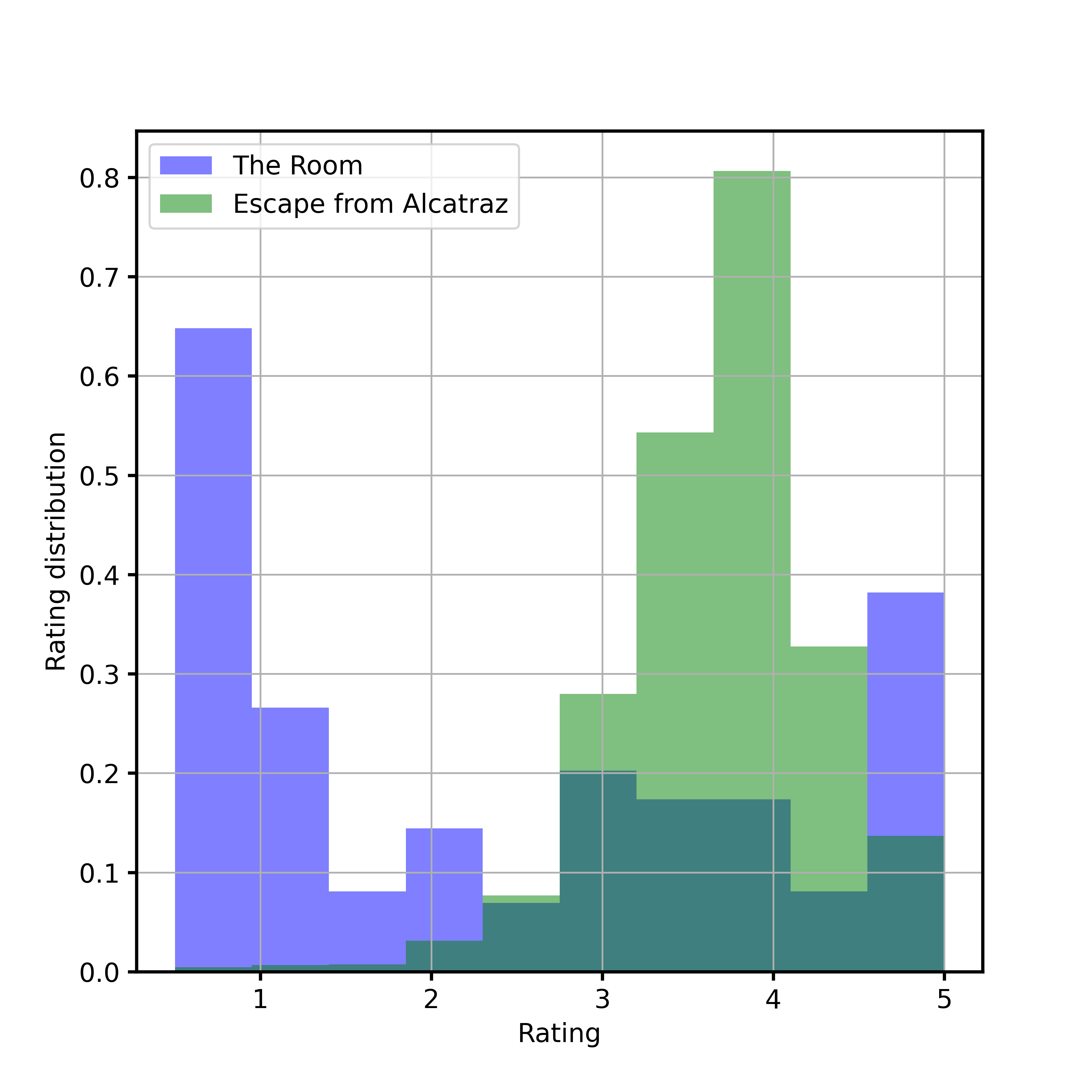
Escape from Alcatraz | 3.78 | 0.67  
The Counterfeiters   | 3.95 | 0.67  
The Lookout          | 3.56 | 0.69  
Wordplay             | 3.81 | 0.69  
Presumed Innocent    | 3.65 | 0.70 

Here you can check the rating distributions: Escape from Alcatraz, The Counterfeiters, The Lookout, Wordplay, and Presumed Innocent. As you can see the rating distributions are pretty concentrated around the average value. Curiously, the least controversial movies are not those with the lowest/highest score, as one would expect from the theoretical upper bound I derived in the last section.

Most controversial movies

Now, we can answer the opposite question and look for the movies that are more controversial. Here instead of looking for the most controversial movies I decided to stratify the search, ie: look for the most controversial movie with an average rating between 1 and 2, with an average rating between 2 and 3, etc.

Range  | Title                   | mean | std  
-------|-------------------------|------|------
(0, 1) | From Justin to Kelly    | 0.99 | 0.85  
(1, 2) | Digimon: The Movie      | 1.98 | 1.39
(2, 3) | The Room                | 2.41 | 1.72  
(3, 4) | Repo! The Genetic Opera | 3.27 | 1.35  
(4, 5) | Heart of a Dog          | 4.08 | 1.25  

This means that the most controversial movie ever is The Room, what a surprise eh? Notice that even The Room is far from the maximum variance one could get, so this means we haven’t seen yet the most controversial movie ever. Who knows what the future holds for us? In the next figure I’ve plotted the variance of the most controversial movies and the theoretical upper bound. We still have a huge margin for controversial movies.

As a last gift, I leave you here the distribution of the two most and least controversial films in history

Conclusions

In this post I’ve studied the topic of controversy in movies from two perspectives: the theoretical one and the experimental one. I derived an upper bound of the “controversiality” of a movie, and then discovered that The Room is the most controversial movie and Escape from Alcatraz is the movie that people agree most about its quality.